Towards Understanding Symbolic AI

All the baselines and Results

Towards Symbolic AI

With the rapid advancement of artificial intelligence, there is a growing interest in symbolic reasoning. This resurgence is particularly significant because humans tend to learn extensively by understanding, identifying, and forming relationships between symbols. Symbolic AI aims to model such processes by examining the relations among symbols and using formal systems—such as logical or probabilistic inference—to discover new symbolic connections.

However, a persistent challenge in symbolic AI lies in the complexity of integrating benchmarks and hypotheses that arise from the study of symbols into modern AI systems. Rather than being clearly defined and embedded, these symbolic components are often entangled within broader architectures. For instance, the grounding problem—how to ensure that symbols carry meaning—offers crucial insight into the semantics and relational structures of symbols, including metaphysical grounding. Analogical reasoning, another key area, involves mapping relationships between symbols metaphorically. This is exemplified by vector-based relational models, such as those found in WordNet or word embedding spaces. In such models, semantic relationships can be captured by vector arithmetic (e.g., the vector from king to queen can be applied to gorilla to yield a new conceptual direction): $P = P_{\text{gorilla}} + V_{\text{queen}}$. This illustrates how symbolic meaning can emerge through transformations in a vector space.

These approaches offer a path toward mapping abstract concepts to symbols. Prior AI systems have explored how internal vector representations may acquire meaning through learning processes (e.g., via toy models), contributing to a deeper understanding of how vectors encode and manipulate conceptual directions.

In contrast, humans have developed rich traditions of dealing with symbols, informed by centuries of philosophical, linguistic, and cognitive research. Symbolic AI can benefit from integrating these traditions, helping large-scale systems like LLMs to better handle symbolic reasoning. This, in turn, could lead to safer, more interpretable, and more efficient model architectures, improved algorithms, and more robust data representations.

Accordingly, the goal of this post is to provide a comprehensive overview of symbolic AI systems, exploring their foundations and offering insights into how they might evolve to support future research and practical applications.

Two Branches of Symbolic AI

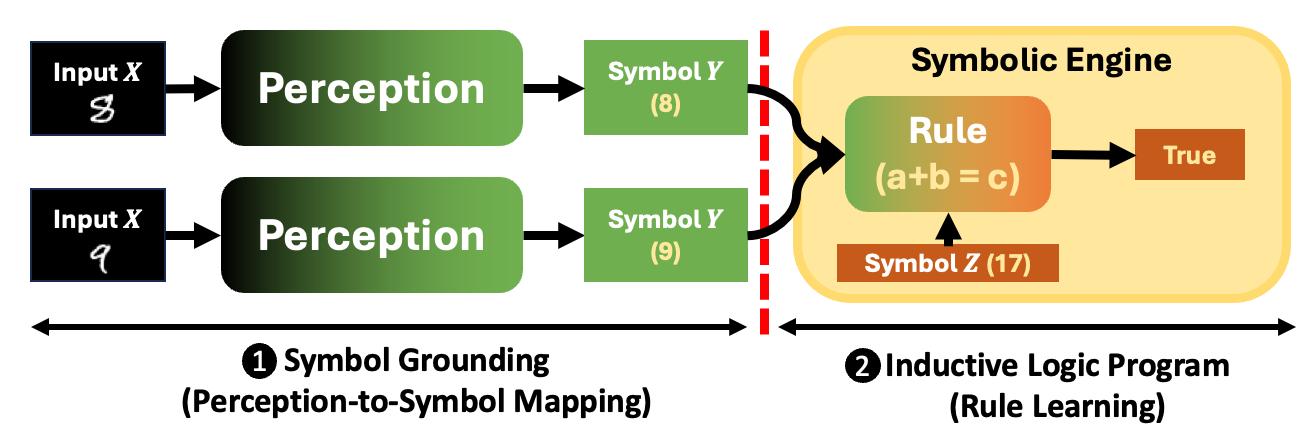
Symbol Grounding (Perception to Symbol Mapping)

Harnad (1990) famously posed the symbol grounding problem: “How can the meanings of words be grounded in anything other than other words?”

What are differences between the symbol grounding problem and classification tasks? (See the footnote Symbol Grounding is about how symbols get their meaning, especially from the world and experience. Classification is about how systems assign labels to data, based on patterns in training data..)

Symbolic logic systems must search over all possible instantiations of symbols, even when the rules are known.

Algorithm Examples

  1. DeepProbLog (Manhaeve et al., 2018) [go below]: The input is processed by a neural predicate digit(Img, Digit), which uses a neural network to produce probabilistic outputs. The error is computed after symbolic reasoning via Prolog, and only the neural network parameters are trained.

  2. Neuro-Symbolic Concept Learner (NS-CL, Mao, 2019) [go below]:
    Given an image and a natural language question, the system first extracts object-level feature vectors from the image. These features are processed through various neural operators (e.g., ShapeOf(obj), ColorOf(obj)) to generate soft attribute estimates. In parallel, the natural language question is parsed into a structured program represented in a domain-specific language (DSL),
    which defines a sequence of symbolic operations (e.g., Filter, Relate, Query). The extracted soft facts—probabilistic evaluations of visual concepts—are then used as inputs to execute the DSL program. This execution is performed not by a traditional symbolic engine, but by a quasi-symbolic executor, also referred to as a neuro-symbolic program executor. This executor evaluates the symbolic program over soft neural outputs,
    enabling differentiable reasoning and end-to-end learning.

  3. NS-VQA (Neuro-Symbolic Visual QA, Yi et al., 2018) [go below]: Uses Mask R-CNN to extract visual features and converts natural language questions into a domain-specific language (DSL) using a GRU-based seq2tree model. The resulting logic program is executed as a symbolic reasoning process via a Python program.

  4. LOGIC-LM (Pan et al., 2023) [go below] A neuro-symbolic reasoning system that combines LLMs with symbolic solvers for faithful logical inference. Shift reasoning execution from LLM to symbolic solvers, leveraging LLMs only for translation (symbol grounding).
    • Problem Formulator – LLM converts a natural language problem into a symbolic representation (FOL, LP, CSP, SAT).
    • Symbolic Reasoner – Deterministic symbolic solver (e.g., Prover9, Pyke, Z3) performs logical inference.
    • Result Interpreter – Maps symbolic result back to natural language.
    • Self-Refiner – Uses solver error messages to revise invalid symbolic forms via iterative prompting.
  5. A-NESI (Krieken et al., 2023) [go below] (Approximate Neurosymbolic Inference)** is a scalable framework that combines neural networks with symbolic reasoning for probabilistic neurosymbolic learning tasks. Unlike traditional methods that rely on exact inference and suffer from exponential time complexity, A-NESI uses neural models to perform approximate inference in polynomial time. It separates prediction and explanation into two neural components trained on synthetic data generated from background knowledge. Additionally, it supports logical constraints at test time through a symbolic pruning mechanism, making it well-suited for safety-critical applications.

Inductive Logic Program (Rule Learning)

🧠 ALGORITHM: DeepProbLog

Mahaeve proposed Probabilistic Logic Programming (DeepProbLog) in 2018. The algorithm trains a neural predicate which is defined by the following format.

nn(m, InputArgs, OutputVar, OutputDomain) :: Predicate.

For example, the digit predicate for an image and symbol digit could be defined by:

nn(mnist_net, [Img], Digit, [0,1,2,3,4,5,6,7,8,9]) :: digit(Img, Digit).

nn(digit_net, [Img], Digit, [0..9]) :: digit(Img, Digit).
nn(op_net, [Img], Op, [+,-,*,/]) :: operator(Img, Op).

solve(E1, E2, E3, Result) :-
    digit(E1, D1),
    digit(E3, D2),
    operator(E2, Op),
    eval(Op, D1, D2, Result).

eval(+, A, B, R) :- R is A + B.
eval(-, A, B, R) :- R is A - B.

🧠 ALGORITHM: NS-CL

Mao proposed Neuro-Symbolic Concept Learner in 2019.

Consider a color vectors:

# Assume 3 color concepts: Red, Blue, Green
v_red   = torch.tensor([0.9, 0.1, 0.0])
v_blue  = torch.tensor([0.2, 0.8, 0.0])
v_green = torch.tensor([0.1, 0.2, 0.9])
concepts = torch.stack([v_red, v_blue, v_green])  # (3, d)

# Object feature (from ResNet)
f_obj = torch.tensor([0.85, 0.15, 0.1])  # example object feature

# Predict color distribution
color_probs = ColorOf(f_obj, concepts)
print(color_probs)  # e.g., tensor([0.81, 0.15, 0.04])

We have a question in the form of natural language: “What is the color of the right object?” It is converted into a DSL form:

# DSL Program:
Program = Query(Color, Filter(Rightmost))

# Step 2: Apply Filter(Rightmost) - select the rightmost object
right_scores = [PositionOf(obj).x for obj in object_features]  # Get x-coordinate
rightmost_index = argmax(right_scores)                        # Index of rightmost object
mask = one_hot(len(object_features), rightmost_index)         # Binary mask for that object

# Step 3: Apply Query(Color) - predict the color of the selected object
selected_feat = weighted_sum(object_features, mask)       # Soft selection
color_probs = ColorOf(selected_feat, color_concepts)      # Probability over color concepts

# Final Answer:
predicted_color = argmax(color_probs)  # e.g., "Red"

🧠 ALGORITHM: LOGIC-LM

Pan et al. introduced LOGIC-LM in 2023. A neuro-symbolic framework that decouples reasoning from language generation by having LLMs generate symbolic representations, and symbolic solvers execute logical inference. LOGIC-LM delegates:

Input:

"Stranger Things" is a popular Netflix show.
If a Netflix show is popular, Karen will binge-watch it.
If and only if Karen binge-watches a Netflix show, she will download it.
Karen does not download "Black Mirror".
"Black Mirror" is a Netflix show.
If Karen binge-watches a Netflix show, she will share it to Lisa.

Question: Is the following statement true, false, or uncertain?  
"Black Mirror" is popular. (A) True  (B) False  (C) Uncertain

Problem Formulator (LLM-generated symbolic form):

Predicates:
NetflixShow(x)        # x is a Netflix show
Popular(x)            # x is popular
BingeWatch(x, y)      # x binge-watches y
Download(x, y)        # x downloads y
Share(x, y, z)        # x shares y to z

Facts:
NetflixShow(strangerThings) ∧ Popular(strangerThings)
∀x (NetflixShow(x) ∧ Popular(x) → BingeWatch(karen, x))
∀x (NetflixShow(x) ∧ BingeWatch(karen, x) ↔ Download(karen, x))
NetflixShow(blackMirror) ∧ ¬Download(karen, blackMirror)
∀x (NetflixShow(x) ∧ BingeWatch(karen, x) → Share(karen, x, lisa))

Query:
Popular(blackMirror)

Symbolic Reasoner Output:

Result: false

Result Interpreter Output:

Answer: (B) False

Self-Refiner (if symbolic execution fails):

Which Symbolic Engine the LLMs use?

An LLM gets a prompt describing the a dedicated task.

🧠 ALGORITHM: A-NESI

🔍 Symbolic Prediction vs Neural Prediction in A-NESI

A-NESI is a scalable framework for Probabilistic Neurosymbolic Learning (PNL) that combines neural perception with symbolic reasoning — without relying on expensive exact inference.

🧩 Core Components

Given an input \(x\) (e.g., images of digits), the perception model \(f(x)\) outputs a belief:

\[P = f(x)\]

where \(P\) is a distribution over possible symbolic worlds \(w\) (e.g., digit pairs like (5,8)).

The symbolic reasoning function \(c(w)\) computes the deterministic output from a world:

\[y = c(w)\]

This captures prior knowledge such as digit summation or Sudoku validity rules.

A-NESI uses a joint factorization of the output distribution:

\[q(w, y \mid P) = q(y \mid P) \cdot q(w \mid y, P)\]

Here, the prediction model \(q(y \mid P)\) generates the output autoregressively, while the explanation model \(q(w \mid y, P)\) identifies the most likely symbolic world that explains the prediction.

To train the system, a belief prior \(p(P)\) is used to generate synthetic training data. The symbolic function \(c(w)\) is applied to each sampled world to produce the supervised output \(y = c(w)\). The prediction model is trained by minimizing the following loss:

\[\mathcal{L}_{\text{Pred}} = \mathbb{E}_{(P, w)} \left[ -\log q(c(w) \mid P) \right]\]

Additionally, the explanation model can be trained using a joint matching loss to align the predicted and true joint distributions:

\[\mathcal{L}_{\text{Expl}} = \mathbb{E}_{(P, w)} \left[ \left( \log q(w, c(w) \mid P) - \log p(w \mid P) \right)^2 \right]\]
Aspect 🧾 Symbolic Prediction 🧠 Neural Prediction
Input \(P = f(x)\) \(P = f(x)\)
Output generation \(w = \arg\max_w \, p(w \mid P), \quad y = c(w)\) \(q(y \mid P) = \prod_{i=1}^{k_Y} q(y_i \mid y_{<i}, P)\)
Reasoning function Uses symbolic reasoning \(c(w)\) No symbolic function; reasoning is learned implicitly
Architecture Sampling + symbolic function RNN-style or Transformer-style autoregressive decoder
Interpretability ✅ High: prediction traceable through \(w\) and \(c(w)\) ❌ Low: no explicit reasoning path
Constraint satisfaction ✅ Yes, via symbolic constraints \(c(w)\) ❌ Not guaranteed (unless symbolic pruning is applied)
Inference speed 🐢 Slower (but scalable with symbolic pruning) ⚡ Fast and parallelizable on GPU
Accuracy on large \(N\) ✅ Stable even for \(N = 15\) ⚠ May degrade at large \(N\) (e.g., MNISTAdd with \(N = 15\))
Training role Validates predictions Trains \(f(x)\) using gradients through \(q(y \mid P)\)
Best suited for Safety-critical, explainable AI Fast inference and large-scale applications

Symbolic pruning in A-NESI improves inference efficiency and ensures logical correctness by eliminating invalid options during the step-by-step generation of symbolic variables. As the model generates each variable (e.g., \(w_i\)), a task-specific pruning function \(s_{y, w_{1:i-1}}(w_i)\) is applied to mask values that violate constraints defined by the symbolic function \(c(w)\). This pruning results in a modified distribution:

\[q'(w_i \mid w_{1:i-1}, y, P) \propto q(w_i \mid \cdot) \cdot s_{y, w_{1:i-1}}(w_i)\]

followed by renormalization:

\[q'(w_i = j \mid \cdot) = \frac{q(w_i = j \mid \cdot) \cdot s(j)}{\sum_{j'} q(w_i = j' \mid \cdot) \cdot s(j')}\]

For example, in MNISTAdd with target sum \(y = 13\), if \(w_1 = 9\), only \(w_2 = 4\) is valid since \(9 + 4 = 13\). All other values are pruned using:

\[s_{y, w_1}(j) = \begin{cases} 1 & \text{if } w_1 + j = y \\ 0 & \text{otherwise} \end{cases}\]

Symbolic pruning is especially important in structured tasks like Sudoku or path planning, and the pruning function must be defined per task using logical rules or constraint checkers.

🧠 ALGORITHM: NS-VQA

NS-VQA (Neuro-Symbolic Visual QA) – Detailed Explanation

The process begins with an input image that contains various objects. These objects are segmented using Mask R-CNN, which detects and outlines each object in the scene. Once the objects are identified, a convolutional neural network (CNN) processes these segments to extract detailed features such as shape, size, material, color, and 3D position coordinates (x, y, z). These features are organized into a structured scene representation table, where each row corresponds to one object and lists its attributes.

Next, the system takes a natural language question as input—such as “How many cubes that are behind the cylinder are large?”—and converts it into a symbolic program. This conversion is performed by a GRU-based LSTM model (a type of seq2tree architecture). The model generates a series of logical operations in a domain-specific language (DSL), forming a symbolic program. For the example question, the generated steps might include filtering for cylinders, identifying objects behind them, filtering those objects for cubes, narrowing down to large ones, and finally counting them.

The symbolic program is then executed using a Python-based symbolic executor. This executor operates on the structured scene representation to perform reasoning tasks like filtering, spatial relation extraction, and attribute comparison. Each operation manipulates the data step by step, narrowing it down based on the program logic. In the example, the system would end up with a set of large cubes behind the cylinder and return the count—say, 3—as the final answer.

NS-VQA achieves remarkably high accuracy on the CLEVR dataset, outperforming most existing methods. When trained with 270 symbolic programs, it achieves 99.8% overall accuracy. It performs especially well in logically intensive tasks such as counting, comparison, and attribute querying, showing that combining neural perception with symbolic reasoning leads to powerful and interpretable AI systems.

🧠 ALGORITHM: Differentiable ILP

Overview
Differentiable ILP (∂ILP) is a neural-symbolic model that learns logical rules from data through differentiable forward chaining. It replaces discrete logical inference with neural computation and enables end-to-end learning without hand-designed rule templates.

Core Components

Advantages

🧠 ALGORITHM: Scallop

Scallop is a neurosymbolic programming language that bridges neural perception and symbolic reasoning through differentiable logic programming. It allows users to define logical rules in a declarative language similar to Datalog and integrate them with neural network models in an end-to-end learnable system. The central idea is to separate perception and reasoning: a neural model processes raw input (such as an image or text) into intermediate symbolic representations, and a logic program applies rules over those representations to produce the final output.

A key feature of Scallop is that while the structure of rules can be given in the form of templates—such as Q(X, Y) :- R(X, Z), S(Z, Y)—the actual mapping of these variables to task-specific predicates (e.g., Q = ancestor, R = parent, S = ancestor) is learned from data. This enables the system to generalize over symbolic patterns without requiring full supervision on internal structures. In most applications, the base predicates like parent, friend, or colleague are defined in advance, and Scallop searches over combinations of those to learn rules that best explain the output.

For example, in a knowledge reasoning task, the model may be asked to infer the ancestor(X, Y) relation. Given known facts like parent(A, B) and parent(B, C), Scallop can learn to compose these into recursive rules that define ancestry. The learning process optimizes both the parameters of the neural perception module and the symbolic reasoning path using a framework based on provenance semirings, allowing gradients to flow from output supervision back through symbolic programs and into the neural components.

Scallop supports recursion, negation, and aggregation in its logic programs, and can be used across a range of domains including visual reasoning, program induction, planning, and reinforcement learning. By combining structured reasoning with perceptual learning in a differentiable and modular way, Scallop enables both interpretability and scalability in neurosymbolic systems.

📦 Example: Scallop Code

// Knowledge base facts
rel is_a("giraffe", "mammal")
rel is_a("tiger", "mammal")
rel is_a("mammal", "animal")

// Knowledge base rule
rel name(a, b) :- name(a, c), is_a(c, b)

// Recognized from an image (neural model output)
rel name = {
  0.3::(1, "giraffe"),
  0.7::(1, "tiger"),
  0.9::(2, "giraffe"),
  0.1::(2, "tiger"),
}

// Aggregation query
rel num_animals(n) :- n = count(o: name(o, "animal"))

🔍 What is Given vs. What is Trained

Component Given (Static) ✅ Trained (Learned) 🧠
Facts (e.g., is_a("tiger", "mammal")) ✅ Provided explicitly in logic  
Rule templates (e.g., Q(X,Y) :- R(X,Z)) ✅ Given as abstract logical structure  
Predicate vocabulary (e.g., is_a, name) ✅ Declared in program or data schema  
Neural predictions (e.g., name = {...}) ❌ Produced by trained neural model ✅ Neural model learns from input data
Rule-body mappings (e.g., Q = ancestor) 🔄 Can be fixed or learned (ILP-style) ✅ Selected based on performance from data
Final prediction (e.g., num_animals(n)) ❌ Derived via symbolic reasoning ✅ Supervised through end-to-end training

🧠 ALGORITHM: pLogicNet

pLogicNet merges symbolic logic (e.g., Markov Logic Networks) with embedding-based models (e.g., TransE, DistMult).

Learning Procedure (Variational EM)

1. E-Step (Expectation)

  1. Use a KGE (Knowledge Graph Embedding) model to infer hidden triples.
  2. Apply predefined logical rules to expand the inferred graph (via the Markov Blanket).

2. M-Step (Maximization)

  1. Update the weights of logical rules using observed and inferred triples.
  2. Optimize the pseudo-likelihood function for probabilistic inference.

Example

(A) Newton — BornIn — UK  
(B) UK — LocatedIn — Europe

Using a composition rule, infer:  
→ Newton — LocatedIn — Europe

Final Score = 0.82 (KGE) + λ × 1.0 (logical rule inference)

References