Mastering Board Games by External and Internal Planning with Language Models

DeepMind

This paper introduces MCTS for board games with pre-trained MAV model. Additionally, they distill the search procedure into the LLM.

• Multi action-value (MAV) model, capable of playing several board games (Chess, Fischer Random / Chess960, Connect Four, Hex) at a strong level.

Reasoning in language models aims to enhance performance on reasoning benchmarks and can be categorized into two approaches:

1. Internal Planning:
   The model develops a plan within the context (e.g., Chain-of-Thought prompting) by autoregressively considering possible steps and their outcomes.

2. External Planning:
   The model generates steps in a neurosymbolic system (e.g., Tree of Thought) with an outer loop explicitly searching over possible step sequences.

The paper explores training language models for both approaches to improve reasoning in sequential decision-making, using board games as the experimental domain.

Summary: Multi-Action-Value (MAV) Model

The MAV model is a Transformer pre-trained on textual game data, designed to function as:

1. World Model:
   • Tracks game states after moves.
   • Predicts legal moves.
   • Detects terminal states.
2. Value Function:
   • Outputs action values as win probabilities.
   • Uses discrete buckets (e.g., 64) to represent win probabilities.
3. Policy Function:
   • Determines the best action for multiple board games.

Key Features:

• State Representation:
  • Textual format tokenizes each board square separately for clarity.
  • Supports standard formats like FEN for chess.
• State Tracking:
  • Tracks transitions using commands like %prev_state and %prev_action.
  • Can predict future states based on chosen actions.
• Value Function:
  • %top_k command outputs a list of legal moves with action values.
  • Configurable to output top-k or all moves, balancing quality and computation.

Improvements:

1. Unified modeling of world state, policy, and action values.
2. Outputs best actions without reliance on external engines.
3. Efficient single-call inference for reduced computational cost.
4. Scalable inference-time computation for higher-quality results.

Datasets:

• Includes game positions from Chess, Chess960, Connect Four, and Hex.
• Data is randomized for training robustness.

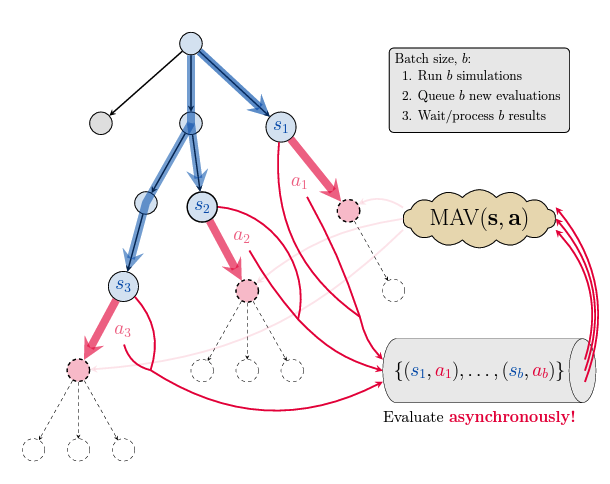
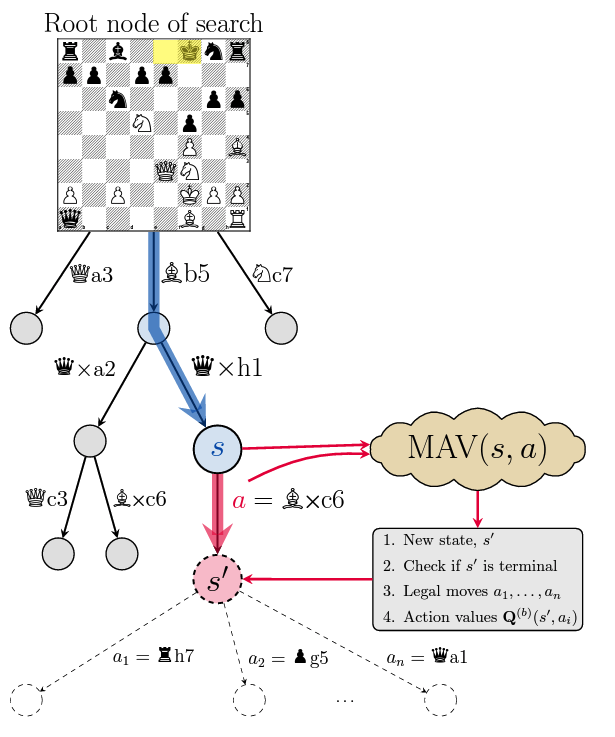
External Search:

• Incorporates Monte Carlo Tree Search (MCTS) for planning.
• Replaces reliance on game engines with learned world modeling.
• Dynamically adapts parameters for optimal decision-making.

Applications:

• MAV handles game-playing tasks like move prediction and planning with minimal reliance on external tools, showcasing advanced integration of internal and external reasoning.

Discrete Representation of Win Rate in MAV Model

The MAV model represents win rates in a discrete form rather than as continuous values. This is achieved through the use of 64 discrete buckets, each represented by a unique token (e.g., <ctrl28> for bucket 28).

Key Details:

• Conversion from Continuous to Discrete:
  • Win probabilities are derived from Stockfish’s centipawn evaluations and then mapped into one of the 64 buckets.
  • For example, the formula used for conversion is:
    [ \text{Win\%} = 50 + 50 \cdot \frac{1}{1 + e^{-0.00368208 \cdot \text{centipawns}}} ]
• Classification Task:
  • By using discrete buckets, the win rate prediction is transformed into a classification task instead of a regression task.

Advantages of Discrete Representation:

1. Stability in Training:
   • Classification tasks are less sensitive to noise compared to regression tasks, leading to more stable training.
2. Efficiency in Inference:
   • Predicting discrete tokens is computationally simpler and faster than predicting continuous values.
3. Improved Differentiation:
   • Discrete buckets allow the model to clearly differentiate between similar values, helping it select the optimal moves.

Example in Chess:

• The discrete buckets ensure that state-action values are encoded in a way that allows the model to predict win probabilities efficiently.
• This approach aligns with similar methods used in other works (e.g., Ruoss et al., 2024) to improve decision-making in game-playing models.

By using this bucketized representation, the MAV model achieves a balance between precision and computational efficiency, enabling better performance in both training and inference.

Explanation of MAV Input/Output Specification

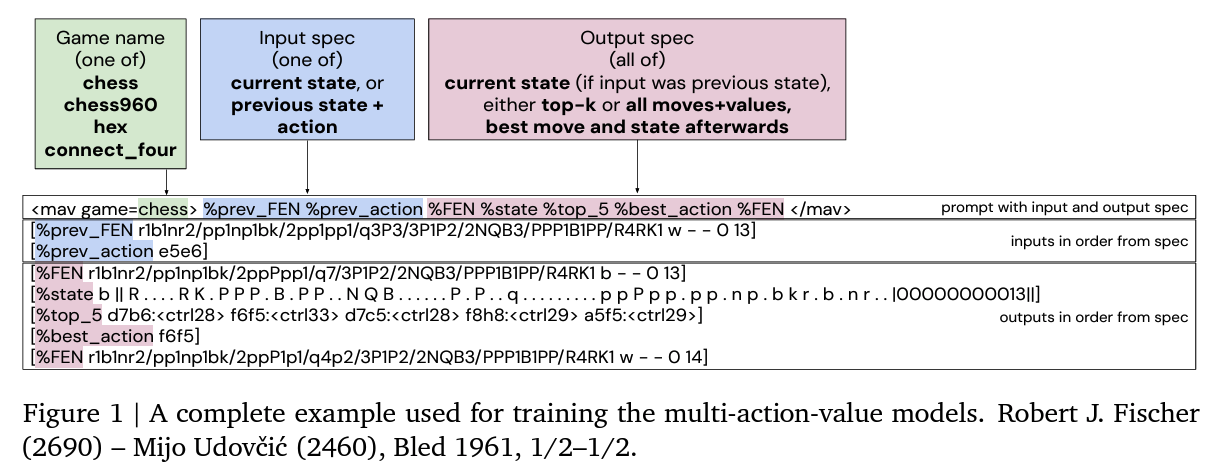
The figure provides an example of how the Multi-Action-Value (MAV) model processes input and output in the context of game-playing tasks, specifically for Chess.

1. Structure Overview

• Game name (green):
  • Specifies the game being played (e.g., chess, chess960, hex, connect_four).
• Input specification (blue):
  • Indicates the format of input, which could be either:
    1. Current state: The game’s current board position.
    2. Previous state + action: The board position before the last move, along with the last move itself.
• Output specification (pink):
  • Specifies what the model should produce, including:
    1. Current state: If the input includes the previous state, this provides the state after the last move.
    2. Top-k moves or all moves + values: A ranked list of legal moves with associated win probabilities.
    3. Best move: The single best move based on the model’s evaluation.
    4. Updated state: The state after the best move is played.

Performance

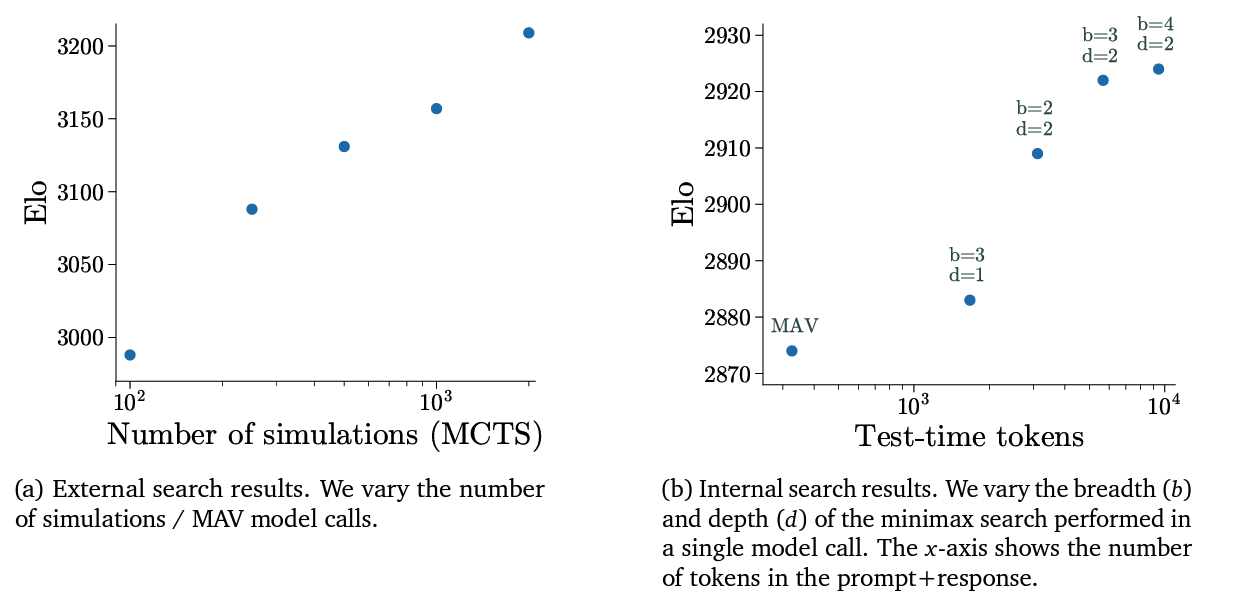
Parallel Search